Rabbits and Recurrence Relations (Rosalind)

    

Halo teman-teman, apa kabar? Kali ini saya ingin membahas sedikit tentang salah satu problem yang ada di web rosalind.info. Judulnya ialah "Rabbits and Recurrence Relations". Sebagai acuan, teman-teman bisa cek dahulu problem yang akan kita bahas (disini). 

Di problem ini kita akan disajikan 2 integer yang mewakili "durasi (dalam bulan)" dan "jumlah pasangan kelinci yang dihasilkan per bulan"; sebut saja n dan k. Tugas kita ialah menemukan total jumlah pasangan kelinci pada bulan ke-n. 

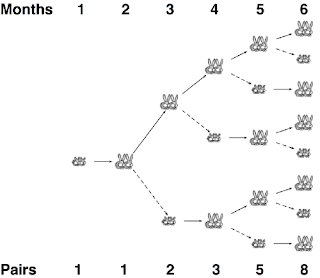
Gambar diatas ialah analogi dari pertumbuhan populasi kelinci.

Untuk mencari jawabannya, seperti yang telah disarankan oleh pembuat problem, kita dapat menggunakan pendekatan dynamic programming. Pada kesempatan ini, saya memakai dynamic programming dengan 2 baris dan n kolom: baris 1 mewakili jumlah pasangan kelinci dewasa (yang bisa menghasilkan keturunan) dan baris 2 mewakili jumlah pasangan kelinci muda (yang belum bisa menghasilkan keturunan); sedangkan kolom (1 ke n) mewakili durasi waktu (dalam bulan). Semakin kolom bergeser ke kanan maka yang terjadi ialah: setiap pasang kelinci dewasa menghasilkan k pasang keturunan, sedangkan kelinci muda menjadi kelinci dewasa.  

Jawaban (total populasi kelinci) dari problem ini terletak di kolom paling kanan pada baris: Kolom paling kanan pada baris 1 mewakili jumlah pasangan kelinci dewasa, sedangkan kolom paling kanan pada baris 2 mewakili jumlah pasangan kelinci muda. 

Berikut kode pengerjaannya dalam bahasa java :

static void solve() {

int n = ni();

int k = ni();

long[][] dp = new long[2][n];

dp[0][0] = 0;

dp[1][0] = 1;

for (int i = 1; i < n; i++) {

dp[0][i] = dp[0][i - 1] + dp[1][i - 1];

dp[1][i] = dp[0][i - 1] * k;

}

out.println(dp[1][n - 1] + dp[0][n - 1]);

}  

Disini saya memakai fungsi ni() untuk meng-input data string. Fungsi tersebut adalah extend dari salah satu sistem input di java, yaitu BufferedReader. 

Sedangkan untuk output-nya saya memakai fungsi out.println(). Fungsi tersebut adalah modifikasi dari fungsi System.out.println()  yang merupakan fungsi default di java. Untuk lebih jelasnya teman-teman bisa melihat kode tambahan untuk memodifikasi fungsi tersebut di versi lengkap kode saya di github. 

Sekian dari saya. Jika teman-teman ingin menanyakan sesuatu, teman-teman bisa menulisnya di kolom komentar. Semoga bermanfaat dan sampai jumpa di artikel berikutnya!

Referensi :

Sumber gambar 1 :https://www.facebook.com/ProjectRosalind/

Sumber gambar 2 :https://medium.com/algorithms-for-life/rosalind-walkthrough-rabbits-and-recurrence-relations-4812c0c2ddb3